DETR 代码解读
Published:
本文从一个CV小白的角度介绍 ECCV 2020 的这篇文章:End-to-End Object Detection with Transformers (github代码)。 该论文首次将 Transformer 引入物体检测领域,具有 end-to-end 的特点。
| End-to-end 可理解为:端对端,即模型的正向训练和反向传播是 一个完整且连续 的过程。举个反例来帮助理解:人体关键点检测时往往需要先框出人体位置,再搜索关键点,分别在两个模型实现。如果这两个模型分别训练完成,那么整体就不是一个“端对端”的模型。 |
概述
物体检测的任务是预测图片中目标物体的边界框(bounding box)及类别(labels)。目前,大多数物体检测的方法会预先构造一系列“参考”,如 proposals, anchors, window centers,然后判断这些参考内有无目标,目标距离参考有多远,从而避免多尺度遍历滑窗造成的时间消耗等问题。输出检测结果后,还需要通过非极大抑制(non-maximum suppression)等后处理步骤消除冗余的边界框。这些过程都需要先验知识,手动设置完成。
DETR 的目的是摆脱上述预处理和后处理步骤的限制,将物体检测视作集合预测问题(set prediction problem)。总体思路是:将训练数据输入 CNN 网络构成的 backbone,得到图像的高维特征 feature map。这些特征作为 Transformer Encoder 的输入,结合图像的位置编码,经过 Decoder 后得到固定数目(大于该数据集最大物体数)query 的特征信息,最后通过前向网络将 query 所包含的信息映射到图片中物体的边界框及标签。
| set prediction problem: set 表示预测值与目标值分别放在两个无序集中,二者之间通过匈牙利算法匹配,保证了“交换不变性”。这种特性使得匹配结果与匹配的先后顺序无关,整个网络可以并行计算,大大提高了计算效率。 |
模型特点
- 基于二分图匹配计算 loss,将预测值稳定地映射到目标值,避免重复预测;
- 与 RNN 模式下通过回归方式检测目标不同,DETR 运用了 transformer 网络,使网络具有并行计算的能力,可同时预测一张图像上的所有物体;
- 省去了需要先验知识的预设参数及后处理步骤,整体具有端对端的特点。
具体实现
如图1所示,DETR 通过以下几部分实现:
- 由卷积神经网络构成的 backbone,用来提取图像的高维特征;
- 由 encoder-decoder 组成的 transformer,用来输出带有物体位置和标签信息的 embeddings;
- 前向网络 FFN 用于将 transformer 输出的 embeddings 映射到物体的边界框及标签概率。
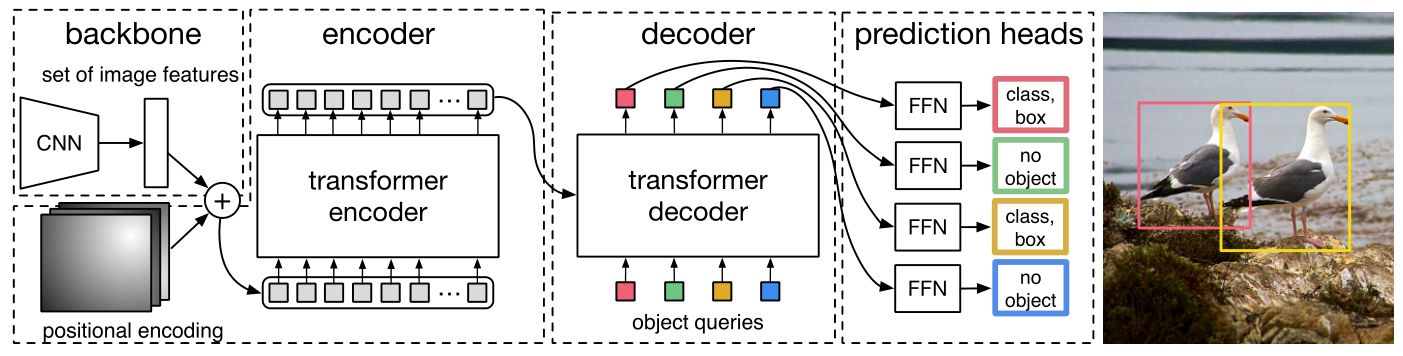
图1:DETR 整体框架
接下来,我们跟着代码来解读 DETR,以 ./d2/models 目录下的模块为单位。这里首先给出如图2所示的流程图,包含了每个模块输入输出变量名及其维度,以供参考。
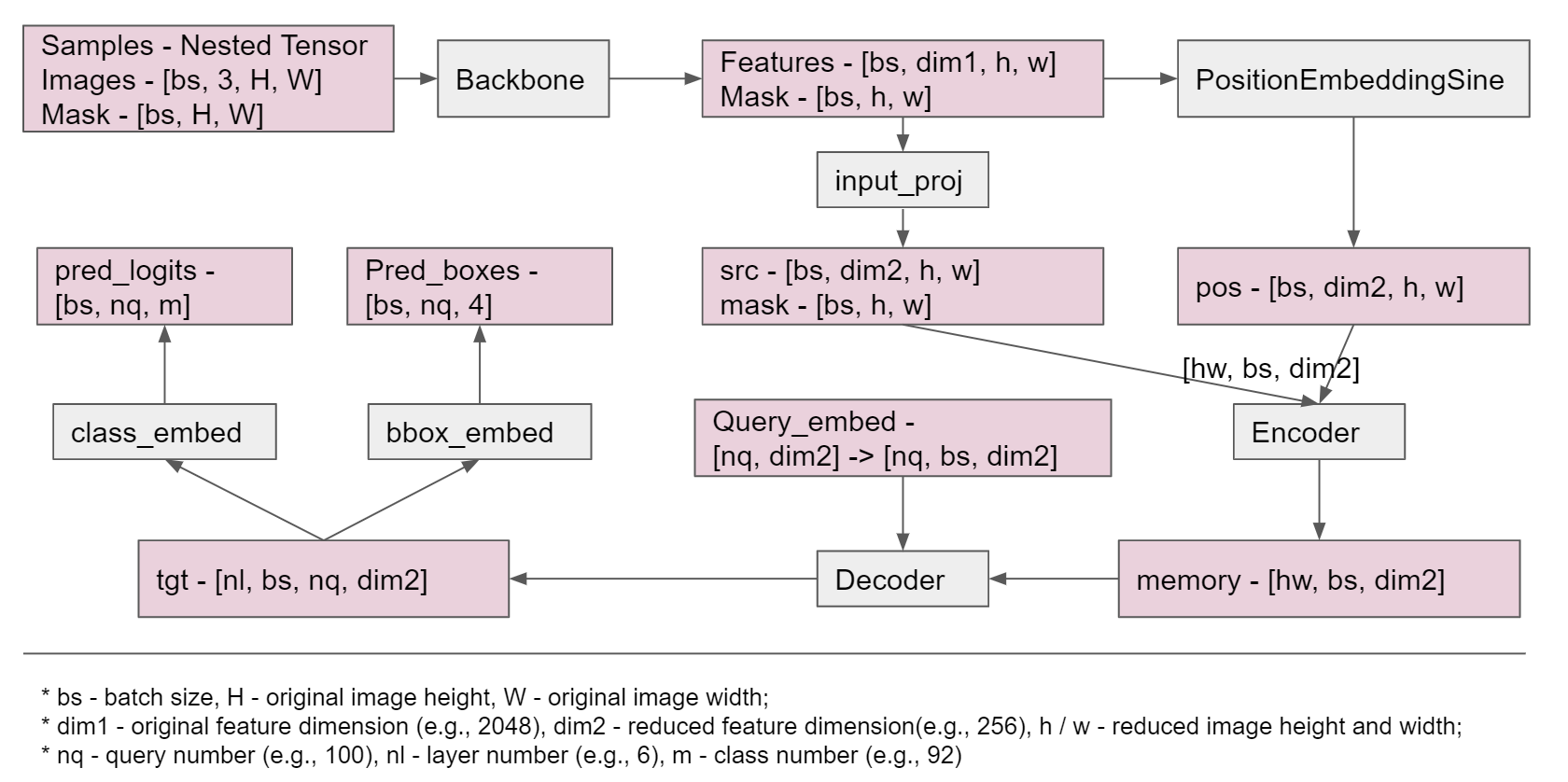
图2:变量维度说明
DETR
首先来看 DETR 中最核心的模块——DEtection Transformer (DETR),以下是该模型的初始化及前向传播过程,部分解读写在注释中。
class DETR(nn.Module):
def __init__(self, backbone, transformer, num_classes, num_queries, aux_loss=False):
super().__init__()
self.num_queries = num_queries
self.transformer = transformer # transformer 模型
hidden_dim = transformer.d_model # 隐层维度,一般设为 256
self.class_embed = nn.Linear(hidden_dim, num_classes + 1) # 全连接层,预测每类的概率
self.bbox_embed = MLP(hidden_dim, hidden_dim, 4, 3) # 多层感知机,用于预测边界框位置
self.query_embed = nn.Embedding(num_queries, hidden_dim) # 网络可学习的参数,含有物体抽象特征
self.input_proj = nn.Conv2d(backbone.num_channels, hidden_dim, kernel_size=1) # 1*1 卷积,用于特征降维
self.backbone = backbone # 主干网络
self.aux_loss = aux_loss
def forward(self, samples: NestedTensor):
if isinstance(samples, (list, torch.Tensor)):
samples = nested_tensor_from_tensor_list(samples) # 将 samples 包裹在 nested_tensor 中
features, pos = self.backbone(samples)
# mask 是所有图像 padding 后的维度(padding 到相同维度)
src, mask = features[-1].decompose() # src [bs, dim, H, W], mask [bs, H, W]
assert mask is not None
hs = self.transformer(self.input_proj(src), mask, self.query_embed.weight, pos[-1])[0]
# transformer 返回 decoder 输出的 query embedding 以及 encoder 输出的 memory, 这里 [0] 表示取 query embedding
outputs_class = self.class_embed(hs) # 将 transformer 输出结果转换为 类 的预测概率
outputs_coord = self.bbox_embed(hs).sigmoid() # 将 transformer 输出结果转换为 框 的位置信息,sigmoid 归一化到 0-1
out = {'pred_logits': outputs_class[-1], 'pred_boxes': outputs_coord[-1]}
if self.aux_loss:
out['aux_outputs'] = self._set_aux_loss(outputs_class, outputs_coord)
return out
这一模型完成了我们在【概述】和【具体实现】中提到的所有过程:输入图像信息 samples,经过 self.backbone 提取特征 features 并获得位置编码 pos ,将特征通过 \(1*1\) 卷积 self.input_proj 降维,并与初始化的 query embedding 一起输入 self.transformer 模块,得到新的 query embedding 特征 hs,最后通过全连接层 self.class_embed 和多层状态机 self.bbox_embed 分别预测每个类的概率 outputs_class 和边界框的位置 outputs_coord。
| 这里需要先解释一下 query 的概念。query 可以粗浅地理解为:一张图上可能出现的最大个数的物体所包含的抽象特征。这个最大个数是一个预设值,原始代码中设置为 100,即作者假设一张图上的物体不超过 100 个。那么每次我们都按图上有 100 个物体去计算,有的 query 预测得到的概率很低,即匹配到背景,被舍弃;有的 query 得分很高,说明他们匹配到了真实物体,被输出。使用 query 的好处在于:网络在学习的过程中主动捕捉了所有物体共有的抽象特征,并使 query 逐渐逼近他指向的物体。这一过程体现了 Transformer 特有的 “自注意力” 特性,与传统方法中通过人为定义锚点等预设值找到物体位置有很大区别。 |
下面再来补充一些 DETR 的代码细节:在 forward 函数中可以看到,模型的输入是一个 NestedTensor,可以理解为将输入的数据 “包裹在” 一个 tensor 中;mask 与图像预处理相关:当一个 batch 中的图像大小不一致时,通过补零的形式将输入样本处理整齐,mask 就是补零后的图像尺寸(没有深度维度),这里我们不做过多关注;输出 out 是一个字典,outputs_class, outputs_coord 都取最后一维的原因是:前面输出的 hs 可能包含了 decoder 每层的输出,而我们只取对最后一层输出做变换后的结果。
Backbone
下面我们看特征提取器 —— backbone 部分。这里作者使用了残差网络 ResNet,默认使用 resnet50。
| 模型的默认参数和设置可以在 main.py 的 args 以及目录 ./d2/configs/xxx.yaml 文件中查看。 |
class Backbone(BackboneBase):
"""ResNet backbone with frozen BatchNorm."""
def __init__(self, name: str,
train_backbone: bool,
return_interm_layers: bool,
dilation: bool):
backbone = getattr(torchvision.models, name)(
replace_stride_with_dilation=[False, False, dilation],
pretrained=is_main_process(), norm_layer=FrozenBatchNorm2d)
num_channels = 512 if name in ('resnet18', 'resnet34') else 2048
super().__init__(backbone, train_backbone, num_channels, return_interm_layers)
由于 Backbone 采用现有的残差网络,结构上没什么太多可解释的内容,这里只对一些设定做简要介绍。初始化 Backbone 时根据输入的网络名创建主干网络。replace_stride_with_dilation=[False, False, dilation] :作者将 backbone layer2 - layer4 卷积层的步长设为 2,以降低输出特征的尺寸,其中最后一层根据 dilation:bool 决定是否采用 “空洞卷积” 代替滑动步长为 2 的卷积。“空洞卷积” 的优势在于感受野(FOV)更大。norm_layer=FrozenBatchNorm2d 表示批规范化使用固定的样本均值和方差,而不是根据训练样本实时更新。因为DETR 的 backbone 使用的是在数据量更大的 imagenet 预训练好的 ResNet,因此在这里就不破坏之前统计好的结果。num_channels 表示主干网络最终输出特征的维度,对于层数较少的 resnet18 和 resnet34,输出维度为 512,其余网络设置为 2048。
原始代码 backbone.py 中还有 class Joiner(nn.Sequential) 这个类,用于将主干网络模型和位置编码模型连接起来。
Positional Encoding
原版 Transformer 主要用于自然语言处理(NLP),通过自注意力机制的应用,提取句子的全局信息,避免了 RNN 网络的顺序结构,使模型并行化训练。但自注意力机制中没有引入单词的位置信息,因此需要通过 “位置编码” 将这一信息补全。
同样的,DETR transformer 模块也无法体现图像每个像素点的位置信息,需要通过位置编码获得。在这里,作者将位置编码从NLP中的 一维 拓展到 二维,同时考虑每个像素点沿 长、宽 方向两个维度的编码。代码中给出了两种编码方式:
- 基于正弦余弦函数的编码:通过计算每个像素点沿 x, y 方向在某一基((1/10000)^(2*i/128))下的正余弦值获得总维度是 256(降维后的特征维度)的位置信息;
- 基于学习的编码:把位置编码作为可学习参数,让网络去学习。 一般使用第一种编码方式。
总结一下,Positional Encoding 的目标是输出维度为 [batch_size, hidden_dim, H, W] 的张量。这一张量通过与 embedding 相加补充图像的位置信息。具体的计算过程见如 PositionEmbeddingSine forward 部分的代码:
class PositionEmbeddingSine(nn.Module):
def forward(self, tensor_list: NestedTensor):
x = tensor_list.tensors # 输入图像
mask = tensor_list.mask
assert mask is not None
not_mask = ~mask
y_embed = not_mask.cumsum(1, dtype=torch.float32)
x_embed = not_mask.cumsum(2, dtype=torch.float32)
if self.normalize:
eps = 1e-6
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
pos_x = x_embed[:, :, :, None] / dim_t
pos_y = y_embed[:, :, :, None] / dim_t
pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
return pos
这里 y_embed, x_embed 类似于 matlab 中使用 meshgrid 构造的二维矩阵,所包含的数值分别沿行、列增加。忽略 batch size 维度,未归一化的 y_embed, x_embed 分别为:\(y\_embed = [[1, 1, 1,...], [2, 2, 2,...],..., [H, H, H,...]]\), \(x\_embed = [[1, 2, 3,...], [1, 2, 3,...],..., [1, 2, 3,...]]\)。self.temperature 是基中分母的大小,一般设为 10000,dim_t 可以视作是基。
最后再提一句为什么采用正余弦的方式进行编码。如图3所示是不同频率的正弦函数的波形,每一个时刻点对应的幅值向量可以视作某个空间点 x 或 y 方向的位置编码。邻近的两个点之间高频分量幅值接近,低频分量幅值有微小差别,距离较远的两个点高频分量的幅值差距也很大。这种编码方式与二进制数的编码也很接近,例如: \([[0,1,0,1,0,1,0,1,...],\\ [0,0,1,1,0,0,1,1,...],\\ [0,0,0,0,1,1,1,1,...],...]\)另外还有一点好处:通过正余弦编码,每个点处的编码信息是正交的!
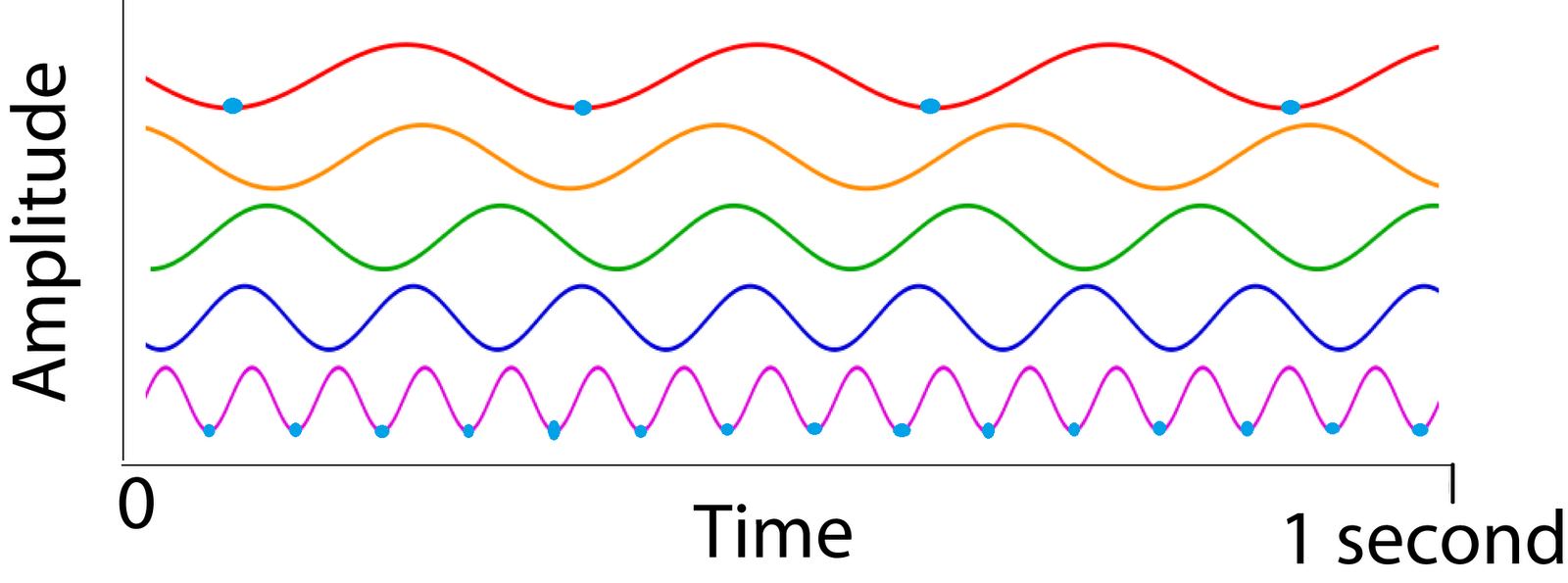
图3:不同频率正弦函数
Transformer
Transformer 分为编码 (Encoder) 和解码 (Decoder) 部分。
DETR 模型的 forward 函数中,通过下面这行代码调用 transformer 模型,并得到 query embedding 的输出:
hs = self.transformer(self.input_proj(src), mask, self.query_embed.weight, pos[-1])[0]
以下是 transformer 的整体结构:
class Transformer(nn.Module):
def __init__(self, d_model=512, nhead=8, num_encoder_layers=6,
num_decoder_layers=6, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False,
return_intermediate_dec=False):
super().__init__()
encoder_layer = TransformerEncoderLayer(d_model, nhead, dim_feedforward,
dropout, activation, normalize_before)
encoder_norm = nn.LayerNorm(d_model) if normalize_before else None
self.encoder = TransformerEncoder(encoder_layer, num_encoder_layers, encoder_norm)
decoder_layer = TransformerDecoderLayer(d_model, nhead, dim_feedforward,
dropout, activation, normalize_before)
decoder_norm = nn.LayerNorm(d_model)
self.decoder = TransformerDecoder(decoder_layer, num_decoder_layers, decoder_norm,
return_intermediate=return_intermediate_dec)
self._reset_parameters()
self.d_model = d_model
self.nhead = nhead
def forward(self, src, mask, query_embed, pos_embed):
# 先将 backbone 得到的特征 src 以及位置编码得到的 pos_embed 的维度从 [BS, C, H, W] 变换到 [HW, bs, C]
bs, c, h, w = src.shape
src = src.flatten(2).permute(2, 0, 1) # HW*BS*C
pos_embed = pos_embed.flatten(2).permute(2, 0, 1)
query_embed = query_embed.unsqueeze(1).repeat(1, bs, 1)
mask = mask.flatten(1) # HW*BS
tgt = torch.zeros_like(query_embed) # 第一层 decoder 输入的 query 初始时是 0
memory = self.encoder(src, src_key_padding_mask=mask, pos=pos_embed)
hs = self.decoder(tgt, memory, memory_key_padding_mask=mask,
pos=pos_embed, query_pos=query_embed)
return hs.transpose(1, 2), memory.permute(1, 2, 0).view(bs, c, h, w)
Transformer 的初始化函数先建一层 encoder_layer,根据是否归一化建立 encoder_norm,并通过 TransformerEncoder 生成 encoder 网络。观察 TransformerEncoder 部分的代码(这里未给出),encoder 网络通过将 encoder_layer 克隆 num_layers 层实现。正向调用中使输入依次通过这些层,得到最终输出 memory。
decoder 网络的建立方法同理。唯一不同的一点是,TransformerDecoder 的初始化函数还有一个参数:return_intermediate,默认值为 False。若该值为真,则 decoder 会返回由每一层的输出 stack 而成的张量,这也就是我们在 DETR 模块中提到的:outputs_class, outputs_coord 都取最后一维的原因。如果不返回每一层的输出,那么最终输出的张量需要通过 output.unsqueeze(0) 加一维,保证输出维度的一致性。
再来看每层 encoder_layer 的细节部分:
class TransformerEncoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
return tensor if pos is None else tensor + pos
# 后 norm 对应的 forward 函数
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
q = k = self.with_pos_embed(src, pos) # 对 encoder 都是 self-attention,所以 q=k
# Self-attention
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
# Add and Norm
src = src + self.dropout1(src2) # shortcut,残差网络的短接结构
src = self.norm1(src)
# FFN
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
# Add and Norm
src = src + self.dropout2(src2)
src = self.norm2(src)
return src
如图4所示,每一个编码层由 self-attention + Add and Norm 层,FFN (Feed Forward Network) + Add and Norm 层串联构成。由于 encoder 没有 embedding 的输入,因此使用 self-attention 模块。参数 query - q, key - k 相同,是高维特征 src 和位置编码 pos 直接相加的结果。这里注意 self-attention 模块的 value 没有引入位置编码的信息。对 self-attention 模块不了解的同学可以移步至 Attention is all you need。
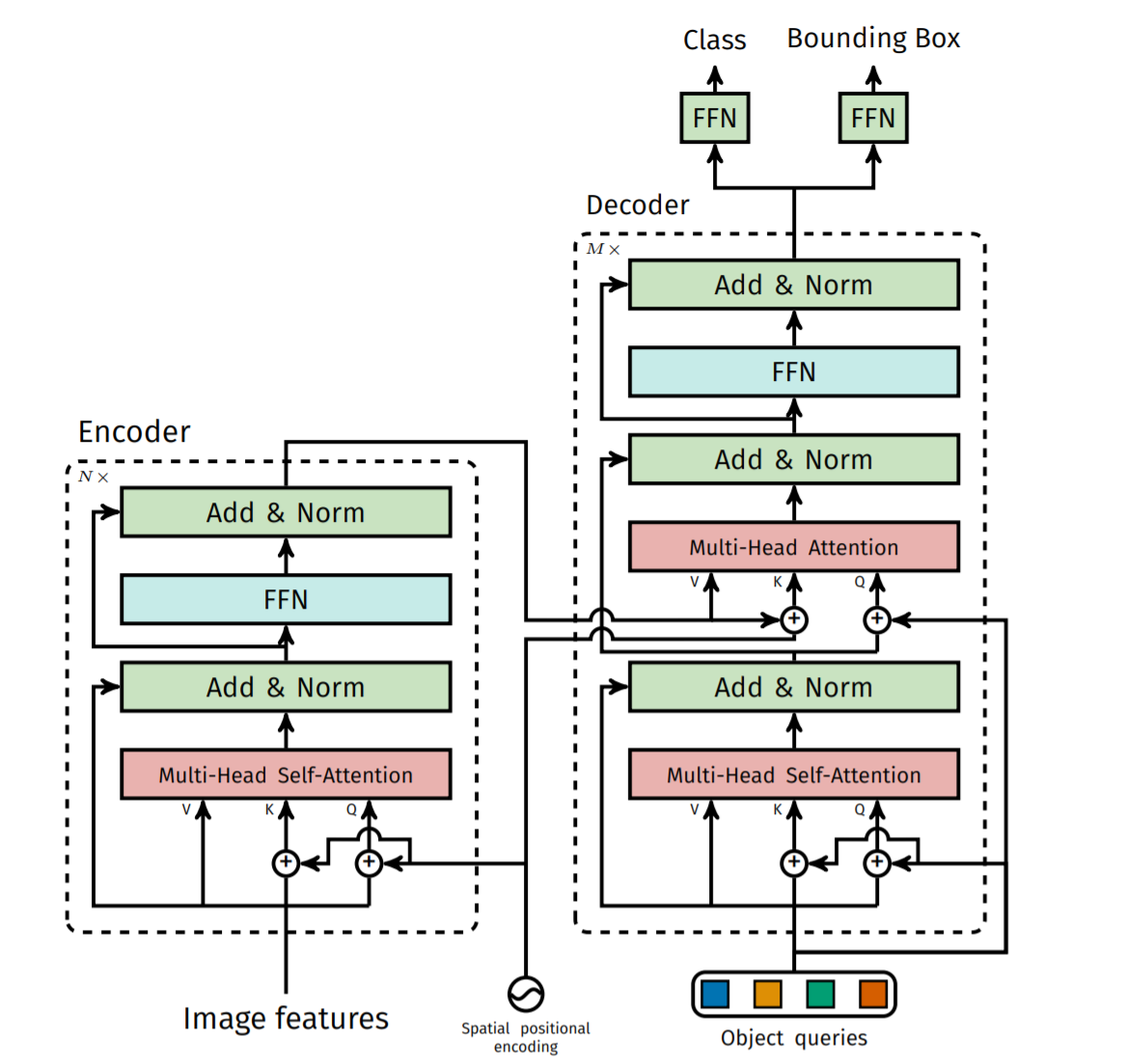
图4: DETR Transformer 结构
解码层与编码层结构略有不同,由 self-attention + Add and Norm 层,Multi-head attention + Add and Norm 层,FFN 层串联构成。这里多了一个 Multi-head attention,是因为 decoder 需要考虑 encoder 输出的 memory 所提供的信息:
class TransformerDecoderLayer(nn.Module):
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
q = k = self.with_pos_embed(tgt, query_pos)
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
# 这里 key,value 引入 encoder 的输出 memory,且 key 包含了位置编码信息
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
return tgt
| 以上前向网络就已经解读完了。下面我们来看模型是如何评估的,具体包括:预测出的 query 如何通过二分图匹配与真值对应;loss 的计算。 |
Matcher
对每个图像,DETR 的输出包括两部分:
- “pred_logits”:维度为 [batch_size, num_queries, num_classes],代表每个 query 预测为某个物体的可能性;
- “pred_boxes”:维度为 [batch_size, num_queries, 4],表示每个 query 预测到的物体边界框的位置。
query 的个数远大于一张图片中可能出现的物体的最大个数,那么如何将预测到的 query 与真值 targets 对应起来呢?DETR 采用 匈牙利算法(Hungarian algorithm)将 query 与真实物体匹配,多余的 query 将与背景噪声空集对应。简单理解,就是计算每个 query 预测为不同类时,在概率层面的代价和在空间边界框层面的代价,找到一种组合方式,使总代价最小。
| 匈牙利算法主要用于解决二分图(Bipartite graph)匹配相关的问题。二分图中的点可归为两部分,每部分内的点互不相连,要求根据题设条件找到最佳连线方式,使代价函数最小。这一算法最早被应用于求解任务分配的组合优化问题。 |
匹配时预测值与真值之间的代价有以下两部分:
- cost_class 直接通过取 “pred_logits” 的相反数获得,即预测是某物体的概率越大,代价越小;
- cost_box 包括 cost_bbox 和 cost_giou。前者计算 l1 距离,后者计算 IoU cost。补充 IoU cost 的原因是:l1 cost 依赖于边界框的大小,IoU cost 则与边界框的尺度无关。 最终加入每种 cost 的权重后,有:final_cost = weight_class * cost_class + weight_bbox * cost_bbox + weight_giou * cost_giou
下面是 HungarianMatcher 的代码实现:
class HungarianMatcher(nn.Module):
def __init__(self, cost_class: float = 1, cost_bbox: float = 1, cost_giou: float = 1):
super().__init__()
self.cost_class = cost_class # 预测概率 cost 对应的权重
self.cost_bbox = cost_bbox # 边界框 l1 cost 的权重
self.cost_giou = cost_giou # IoU cost 的权重
assert cost_class != 0 or cost_bbox != 0 or cost_giou != 0, "all costs cant be 0"
def forward(self, outputs, targets):
bs, num_queries = outputs["pred_logits"].shape[:2]
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1) # [batch_size * num_queries, num_classes]
out_bbox = outputs["pred_boxes"].flatten(0, 1) # [batch_size * num_queries, 4]
tgt_ids = torch.cat([v["labels"] for v in targets])
tgt_bbox = torch.cat([v["boxes"] for v in targets])
cost_class = -out_prob[:, tgt_ids] # 只提取目前出现过的 class 处的 prob,其余的不需要参与匹配
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1) # L1 cost
cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox)) # giou cost
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
C = C.view(bs, num_queries, -1).cpu()
sizes = [len(v["boxes"]) for v in targets] # sizes 存储每个 batch 内物体的个数
# for i, c in enumerate(C.split(sizes, -1)) -> bs * num_queries * [num_target_boxes in image0, num_target_boxes in image1,...]
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]
最终返回的 indices 是一个 list,储存了每对匹配到的 query 和 object 的 index 构成的 tuple。
| 讲到这里已经进入本篇 blog 的尾声了,再坚持一下!!冲!! |
SetCriterion
模型正向过程的最后阶段,找到了预测值和真值之间最佳匹配方式。这时便可以计算这个样本的 loss 了。 模型 loss 的计算位于 ./d2./models/detr.py 中的 SetCriterion 类。与 Matcher 中相同,loss 同样包括两部分:loss_labels 和 loss_boxes。需要注意的是,不同于匹配时使用的 cost_class,计算模型预测概率的 loss 时,用到了 negative log likelihood loss (NLL loss),其实就是计算交叉熵(cross entropy)。
有了 loss,模型便可以通过反向传播优化整个网络的参数啦~
总结
以上是我对 DETR 的全部理解,包含 DETR 的应用背景、基本原理、实现过程。
希望大家能有所收获!
