DTR 论文解读
Published:
本文介绍 ICLR 2021 的这篇文章:Dynamic Tensor Rematerialization (github代码)。 该论文提出的 DTR 策略实现了在动态计算图上 tensor 的重计算,可以保证训练过程中显存占用始终小于某一阈值,为机器显存受限时使用更大的 batch size 提供了可能。
概述
在深度学习领域,增大模型参数量是提升模型表现的重要方法之一。大模型的训练往往依赖于充沛的显卡支持,由内存不足引发的问题将会限制这一领域的发展。设置梯度检查点(gradient checkpointing)可以有效缓解显卡内存的压力。在模型训练的第一阶段——正向计算中,有大量中间变量被保存。事实上,这些变量中的很大一部分生成后并不会很快再被用到,直到进入反向传播时才有用处。因此我们可以在正向计算过程中释放一部分变量的显存,在反向传播时重新计算这些变量的值。通过这种 “以时间换空间” 的方式,减少显存占用,增大 batch size,为在有限的显存上训练大模型提供可能,这就是梯度检查点的基本思想。
目前深度学习中使用的梯度检查点主要针对静态图,这种 “define-and-run” 的模式需要提前获取模型的计算图,并在此基础上对 tensor 的释放(eviction)和重计算(rematerialization)做出规划。越来越多的框架开始支持动态图模式(”define-by-run”),模型的计算图随输入数据而改变,因此较为灵活自然。DTR 的目的便是摆脱静态图的限制,使模型在动态图训练时能自动对显存内的 tensor 释放和重计算,最大限度地利用显存资源。
| 这里简单介绍 动态计算图和静态计算图 的概念。 动态计算图的计算流与输入内容相关。每次运行依赖于当前输入,比较灵活,比如可以由运算中的某个中间结果决定接下来进行哪个分支。但因为没有全局的图信息,失去了很多优化机会,因此速度不如静态计算图。目前 PyTorch 使用动态图机制。 静态计算图的计算流与输入类型相关。根据输入类型和计算图编译出相应的执行程序,即先搭图,后计算。高效,但不够灵活。TensorFlow 使用静态图机制。 |
DTR 特点
- 实时管理显存中的 tensor,维持显存占用在一定阈值以下;
- 设计了一种启发式策略,综合考虑 tensor 在显存中停留的时间、占用的显存大小及重计算的开销,以给出当前最适合被释放的 tensor;
- 使用并查集维护 tensor 之间的联系,提出一种近似精准的 neighborhood set 计算 tensor 的最大重计算开销。
具体实现
DTR 可以看作是在动态图上智能管理 tensor 显存,对 tensor 进行分配、读取、释放、销毁等操作的 “监控+管理器”。
当需要为某个 tensor 分配显存时,DTR 首先检查当前是否有足够空间容纳这个 tensor。如果空间足够大,那么直接分配显存,并为当前变量初始化计算路径等元数据,以供后期重计算使用。若显存不够,则根据启发式策略循环选取并释放当前显存中 cost 最小,也就是最适合被释放的 tensor,直到足以容纳新的 tensor。当要获取某个 tensor 时,先检查目标 tensor 是否位于显存中。如果被释放掉了,那么需要根据元数据中的计算路径重计算生成这一 tensor。需要注意的是,重计算的过程可能触发更多变量被重计算。
我们以原论文图1右下角的计算图及左下角的执行过程为例详细说明。
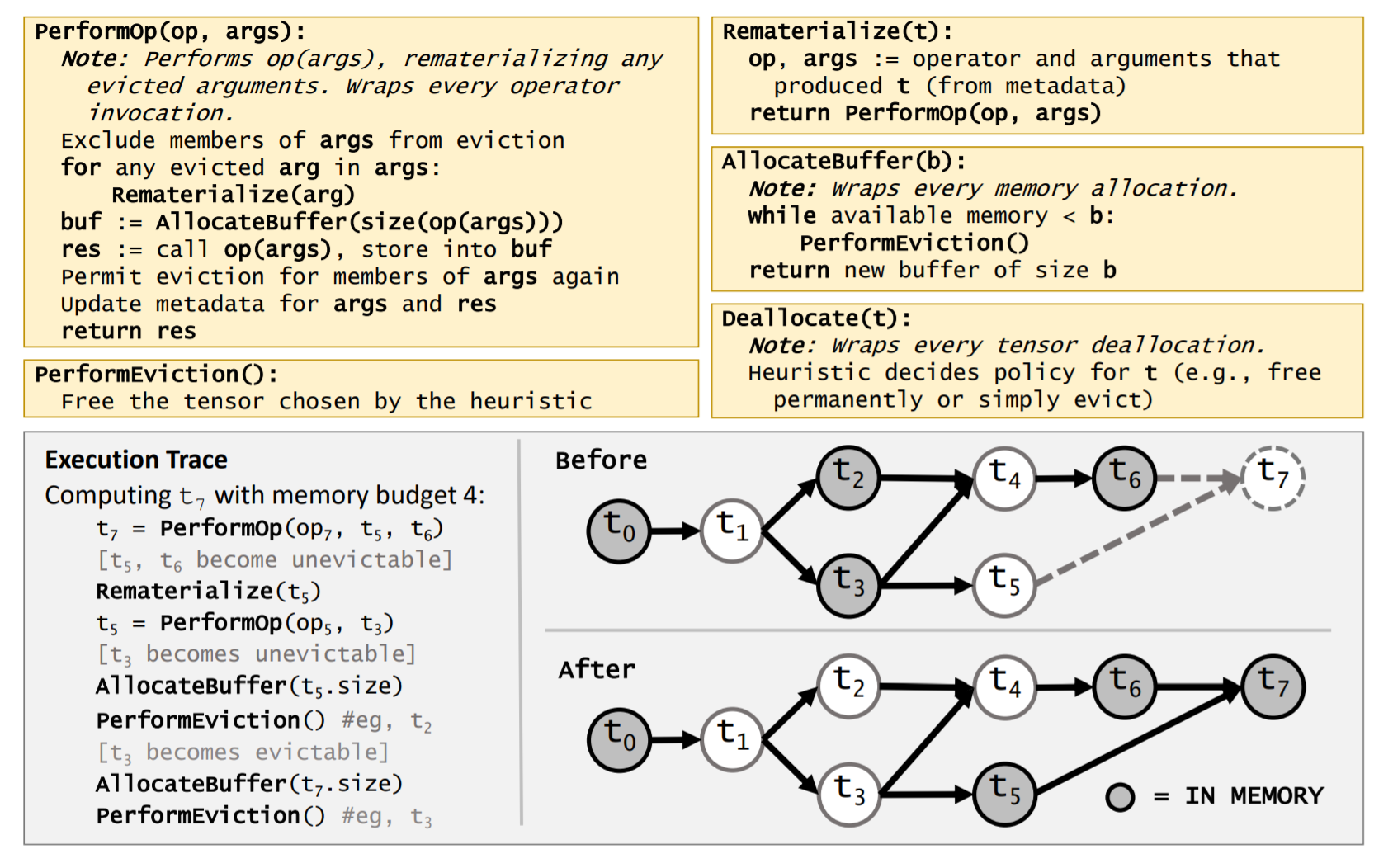
图1:DTR 伪代码及运行示例
假设当前显存只允许 4 个 tensor 存在。图示的计算图中,t0, t2, t3, t6 为目前在显存中的变量。当我们要从 t5, t6 生成 t7 时,首先需要根据 t3 重计算 t5,因此 t3 此时被打上 “不可释放” 的标签。由于显存已满,此时需要启发式地找到最佳 tensor(此时是 t2)释放掉,再生成 t5。这时 t3 暂时不再需要,因此解除 “不可释放” 的标签。同样的,为了给 t7 分配显存,DTR 会首先释放 t3 这个最优 tensor,再生成 t7。
接下来,我们将对 DTR 的启发式算法、用于测试性能的 Simulator、以及在 PyTorch 的原型实现做介绍。
Heuristics
DTR 解决的核心问题之一是:如何自动、高效地从当前位于显存中的所有候选变量找到最适合被释放的 tensor。
DTR 从三个方面对 tensor 进行评估:
- staleness, s(t),上一次访问到现在的时间间隔;
- memory, m(t),占用显存的大小;
- cost, c0(t),生成这一 tensor 消耗的时间。
综合考虑这三方面因素,我们希望被释放的 tensor 最久没用过、占用的显存最大、计算开销最小。因此每个 tensor 的代价可以由$c_0(t)/s(t)/m(t)$表示。但事实上,每个 tensor 的计算开销不仅与生成这一 tensor 的 op 的运行时长有关,还与和它关联的变量(用于生成这一 tensor 或由这一 tensor 生成)相关。比如图 1 中 t7 的生成依赖于 t5 和 t6。由于 t5 不在显存中,t7 的计算开销也应该包含 t5 的生成时间(如果用于生成 t5 的变量 t3 也被释放,那么也应该包含 t3 的生成时间,即时间消耗是呈链式逐层累积的)。DTR 把这些邻近变量中被释放的那部分元素放入一个集合:evicted neighborhood e*(t),定义 projected cost, $c(t) = c_{0}(t)+\sum_{t^{\prime} \in e^{*}(t)} c_{0}\left(t^{\prime}\right)$。于是,理想情况下的 heuristic 被定义为: \(h_{\mathrm{DTR}} \stackrel{\text { def }}{=} \frac{c_{0}(t)+\sum_{t^{\prime} \in e^{*}(t)} c_{0}\left(t^{\prime}\right)}{m(t) \cdot s(t)}\)
上述对 heuristic 的计算虽然精准,但维系集合 e* 的开销将随着变量动态释放和重计算增大。DTR 提出用并查集(Union-find set)管理变量之间的依赖关系,用 $h_{DTR}^{eq}$ 近似取代 $h_{DTR}$。具体做法如下:
如图 2 所示,给定当前内存依赖图(storage dependency graph,这里以 storage 而不是 tensor 判断依赖关系的原因是:很多 tensor 可能指向同一块 storage,具体会在 Simulator 一节说明)$G = (V,E)$,首先忽略依赖关系的方向性得到 $\tilde{G}$;找到所有被释放的变量,则每个被释放且连通的 tensor 构成一个集合,称为一个 evicted component。每个 evicted component 内的元素共享一个 cost,即集合内所有元素的 cost 之和。图 2 中共有 3 个 components,其中有 2 个与我们关注的节点(storage)相连(绿色区域)。我们只需要运用并查集,动态地维护这些 evicted components,就可以计算 \(h_{\mathrm{DTR}}^{\mathrm{eq}} \stackrel{\text { def }}{=} \frac{c_{0}(t)+\sum_{t^{\prime} \in \tilde{e}^{*}(t)} c_{0}\left(t^{\prime}\right)}{m(t) \cdot s(t)}\) 了。
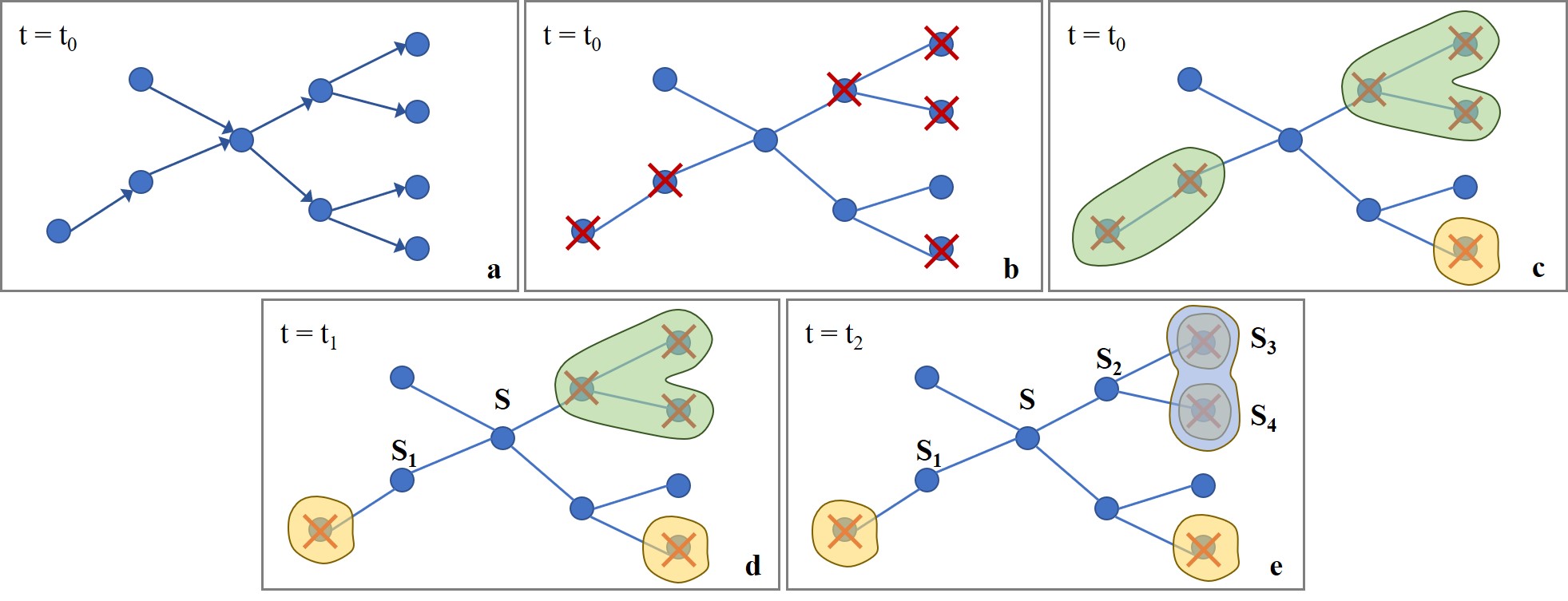
图2:$h_{DTR}^{eq}$计算及近似。
这里需要注意两点:
- 使用 $h_{DTR}^{eq}$ 为什么高效? 应用并查集后,每次只需要搜索与当前 storage 节点相连的 evicted component,不再需要 “顺藤摸瓜”(字面意思)依次搜索该 storage 前后路径上所有被释放的 tensor;
- $h_{DTR}^{eq}$ 为什么是对 $h_{DTR}$ 的近似? 与并查集本身的局限性相关 —— 并查集不支持分割操作。当变量被重计算后,我们需要更新 evicted components,同时修改这些 components 的 cost。在 Simulator 中,分割通过如下操作实现:对某个 Storage 节点 S,$\text{S.set.cost} := \text{S.set.cost} - \text{cost(S)}, \text {S.set}:=\emptyset$。这样的操作可能导致虚假连接(”phantom connections”)出现。
仍然以图 2 为例。假如 $t = t_1$ 时刻重计算 S1 节点,更新并查集后不会出现 cost 出错的问题;$t = t_2$ 时刻重计算 S2,此时我们会发现,尽管 S3 和 S4 在更新后各自独立形成一个新的 evicted component,但并查集仍然将这两个 tensor 连接起来(一个蓝色区域而非两个独立的黄色区域),这就是错误的来源。DTR 的实际测试显示,这样的近似在 Simulator 和 PyTorch 原型中都能得到不错的结果(work well~)。
| 这里简单介绍 并查集 的概念。 并查集可以管理一系列不相交的集合,支持集合的合并和元素的查询,因此常用于维护连通的无向图,判断两个点是否在同一连通块内。每个集合用其中的一个元素代表,该元素称为代表元。一个集合内的所有元素形成以代表元为根的树形结构。但需要注意的是,并查集的算法不支持集合的分割。 |
除了 $h_{DTR}$ 和 $h_{DTR}^{eq}$,原论文还对比了几种其他的 heuristic,如 $h_{\mathrm{DTR}}^{\text {local }} \stackrel{\text { def }}{=} \frac{c_{0}(t)}{m(t) \cdot s(t)}$, $h_{\mathrm{LRU}}(t) \stackrel{\text { def }}{=} \frac{1}{s(t)}$, $h_{\text {size }}(t) \stackrel{\text { def }}{=} \frac{1}{m(t)}$1, $h_{\mathrm{MSPS}}(t) \stackrel{\text { def }}{=} \frac{c_{0}(t)+\sum_{t^{\prime} \in e_{R}(t)} c_{0}\left(t^{\prime}\right)}{m(t)}$2。
DTR Simulator
下面我们看测试 DTR 的仿真实验。
首先,原论文记录了不同模型在 PyTorch 上训练时的 log,包含运行指令、tensor 相关的元数据和操作(如获取 tensor 大小、计算时间、上层 tensor)、及显存重分配等信息。每个模型的日志保存在源码./simrd/logs/目录下,如resnet32-56-9000000000.0-2020-10-1-13-3-30-default.log文件保存了 ResNet-32 的训练过程,以该文件中前几行为例:
{"ANNOTATION":"START","INSTRUCTION":"ANNOTATE"}
{"INSTRUCTION":"CONSTANT","NAME":"x7690"}
{"INSTRUCTION":"MEMORY","MEMORY":"1728","NAME":"x7690"}
{"DST":"x7691","INSTRUCTION":"COPY","SRC":"x7690"}
{"INSTRUCTION":"RELEASE","NAME":"x7690"}
这几行日志记录了一个变量的读入、拷贝和释放。 在 START 后,”CONSTANT” 指令表示当前变量 t 是从外部定义的常量(与计算得到的变量相区别),以 “NAME” 中的字符串 “x7690” 作为标识。”CONSTANT” 后紧跟 “MEMORY” 指令,记录 t 占用的内存大小。”COPY” 指令表示将 “SRC” 中的值拷贝到一个新的变量 “DST”,这一操作后对 “x7690” 这一变量的引用(refs(t))将会自动加一。随后 “RELEASE” 释放该变量。
除了上述几行日志中的指令,还有 “ALIAS”, “CALL”, “MUTATE”, “COPYFROM” 等指令,分别表示:创建别名、对输入变量执行某一操作、in-place操作、将某一变量的值赋给一个已有的变量。 这些日志中的指令信息被 “重放” 给 DTR Simulator,DTR 根据当前显存情况,动态实现 tensor 的管理。源代码./simrd/simrd/parse/parse.py负责解析 log 文件中的指令,读取并判断逻辑,最终将所有指令依次放入图的属性 schedule 中。
由于 DTR 根据 PyTorch 框架下模型的日志进行测试,因此 Simulator 的实现与 PyTorch 的很多特性相关。在 PyTorch 中,一块地址可以被很多个 tensor 同时 “view”。这些变量中除了真正被分配了这块显存的 tensor 之外,其余都可以视为 alias。所以 Simulator 中定义了 Storage 这一概念来管理地址,作为 DTR 直接操作的对象,由./simrd/simrd/tensor.py Storage 类实现。
| Python 中 Aliasing 现象可以由如下操作实现: Basic slicing and indexing, as_strided(), detach(), diagonal(), expand(), expand_as(), permute(), squeeze(), transpose(), unfold(), view(), split(),... |
我们来看 Storage(S) 支持的操作:
| Operation | Output | Explanation |
|---|---|---|
| size | $\mathbb{N}$ | 占用的空间(bytes) |
| root | Tensor | 计算这一 tensor 时分配了这块地址 |
| tensors | List[Tensors] | 所有 view 这块地址的 tensors |
| resident | bool | 如果未被释放则为 True |
| locks | $\mathbb{N}$ | 被锁的次数(当前有多少变量的计算依赖于该 storage) |
| refs | $\mathbb{N}$ | 所有依赖于指向这块地址的 tensor 的操作数,$\text{refs}(S) = \sum_{t \in \text{tensors}(S)} refs(t)$ |
仅当 S 在显存中,且 locks(S) == 0,S 才可能被释放。
在 Storage 的基础上,原论文还定义了 Tensor 类和 Operator 类。其中 Tensor 类支持的操作有:
| Operation | Output | Explanation |
| op | “parent” operation | 生成该 tensor 的操作 |
| refs | $\mathbb{N}$ | 依赖该 tensor 的操作数 |
| size | $\mathbb{N}$ | 如果 t 是别名,则 $\text{size}(t) = 0$,否则为 $\text{size}(\text{storage}(t))$ |
| defined | bool | 仅当 storage(t)==True 且执行过 op(t) 才为 True |
Operator 类用于记录算子的信息(算子名称、运算时间、输出变量的大小、输入变量是否为别名)。
以上就是 DTR Simulator 基于模型在 PyTorch 下的训练日志,进行测试所依赖的几个基本类。除此之外,还有几个重要的类用于实现动态重计算的功能。如./simrd/simrd/parse/graph.py中的 Graph, 记录和维系变量之间的依赖关系;./simrd/simrd/runtime/runtime.py中的 TelemetrizedRuntimeBaseRuntime,动态管理 tensor,实现 tensor 的分配、释放、重计算等操作;./simrd/simrd/heuristic/heuristic.py中的 Heuristic 计算每个 Storage 的代价,并给出代价最小的 Storage。
PyTorch prototype
DTR 也在 PyTorch 上做了修改。根据原论文github中的说明,修改是以“补丁”的形式添加到 PyTorch 框架中的,使用者需要先将 PyTorch 切换到 DTR 修改的 PyTorch 版本,将补丁上传,再编译。下面是lz编译时遇到的小问题及解决方法。
| 补丁中使用C++14,而C++14对std::tuple的构造函数是显式的,因此无法通过 copy-list-initialization 生成 tuple。如 CheckpointTensorImpl.cpp 第127行 PerfStats::TimerStats stats = { name , start, now, elapsed }; 我们暂且通过改为如下代码解决报错,完成编译。 PerfStats::TimerStats stats{ name , start, now, elapsed }; 在 dtr_code/dtr_pytorch/aten/src/Aten/native/Checkpoint.cpp 中很多函数直接返回 copy-list-initialization 生成的 tuple,也可以通过类似的方法解决。 |
DTR 为 PyTorch 中已有的 tensor 定义了一个 wrapper - CheckpointTensor,用于记录生成 tensor 的算子以及其他元数据(如上次访问的时间和计算开销)并将 tensor 在实时系统中注册。CheckpointTensor 可以将包裹的 tensor 从显存中释放,保留计算路径以便后期重计算。新增加的 “checkpoint()” 函数可以将普通 tensor 包裹成 CheckpointTensor,”decheckpoint()” 可以将普通 tensor 从 CheckpointTensor 中提取出来。
DTR 的 runtime 通过单例模式实现。程序开启后,runtime 维护所有 CheckpointTensors 和用于计算 $h_{DTR}^{eq}$ 的 evicted components。在对 CheckpointTensor 的每次操作前,runtime 检查当前显存是否超出阈值,若超出,则启发式地释放 CheckpointTensors。原论文在 PyTorch 上实现的 DTR 原型支持 tensor 的 in-place 操作、别名现象、及多输出运算。
除此之外,论文还提出了两点 近似 用于优化搜索空间:
- 忽略小的 tensor,当 tensor 大小小于当前候选 tensor 平均大小的 1% 时,不主动释放这一 tensor;
- 每次随机选取 sqrt(n) 个 tensor 作为候选集(其中 n 为候选 tensor 的个数)。
结果
下面根据原论文的一些图来看 DTR 的结果。
Fig. 5.
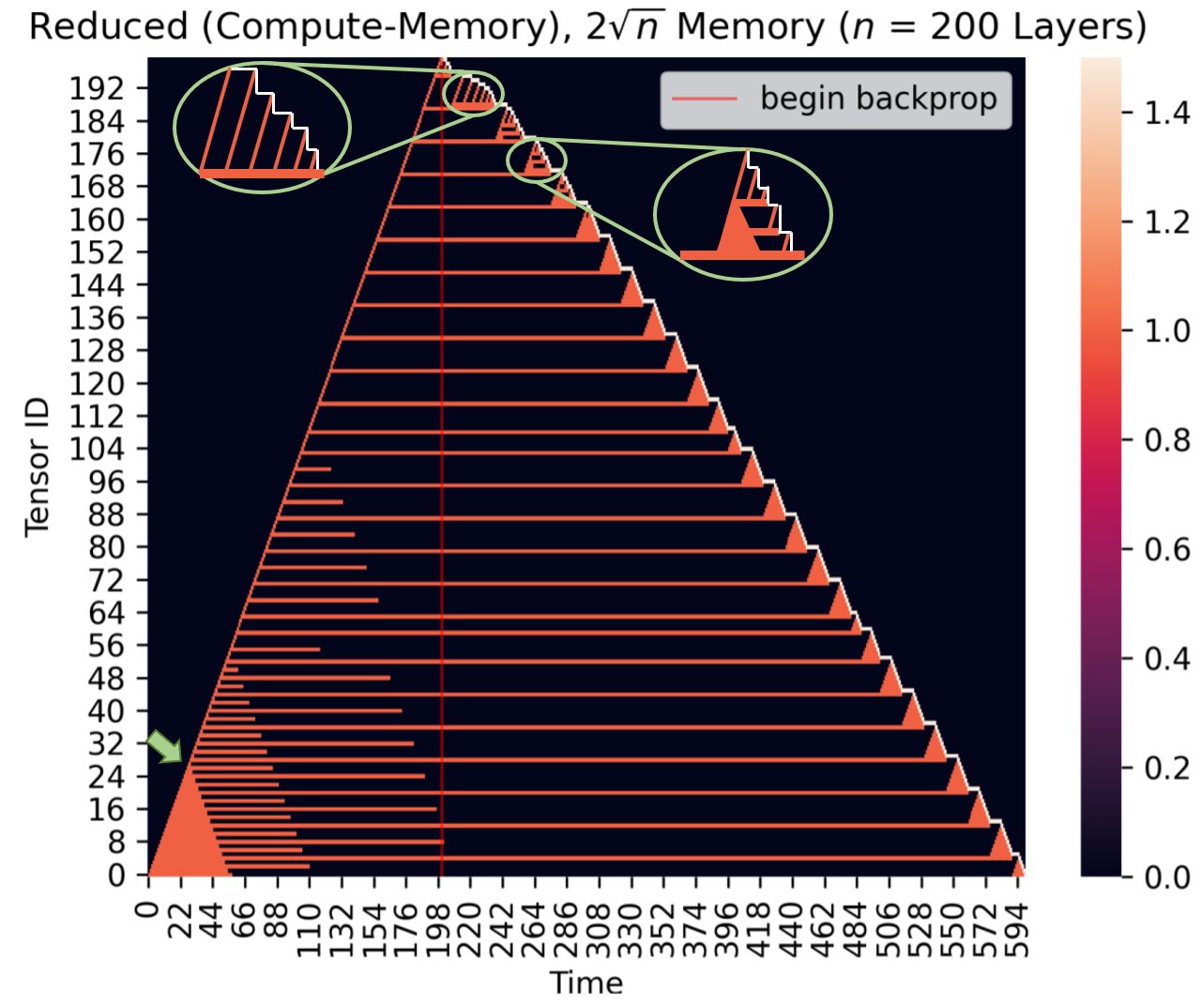
图3:(改自原文Figure 5)正向计算和反向传播过程中 tensor 生命周期示意图。
上图清晰地展示了一次正向计算和反向传播过程中,所有 200 个 tensors 的生命周期。横轴表示时间,纵轴表示 tensor id。随着时间增加,一开始的显存容量足够大。假如我们平移 y 轴,会发现左侧的区域成一个实心的直角三角形,或者我们称为“密集三角形”。此时所有变量都在显存中。直到第一个绿色箭头指向的时刻,显存不够容纳新的变量,出现了第一轮的释放。所有横贯“大三角形”的红色实线表示几乎均匀分布的 checkpoint tensors。在反向传播之前,“密集三角形”的密度越来越小。开始反向传播后,每计算一次梯度,可以 banish 2个 tensor(这两个 tensor 分别存储梯度值和中间变量值),遇到 checkpoint tensor 时,连同检查点一起释放。从两个放大的绿色圈内,可以观察到:随着BP的进行,越来越多的变量被释放,显存中可容纳的变量增多。从梯度检查点还原变量的过程不再需要生成一个就释放一个,而是重新出现了“密集三角形”。
Fig. 2.
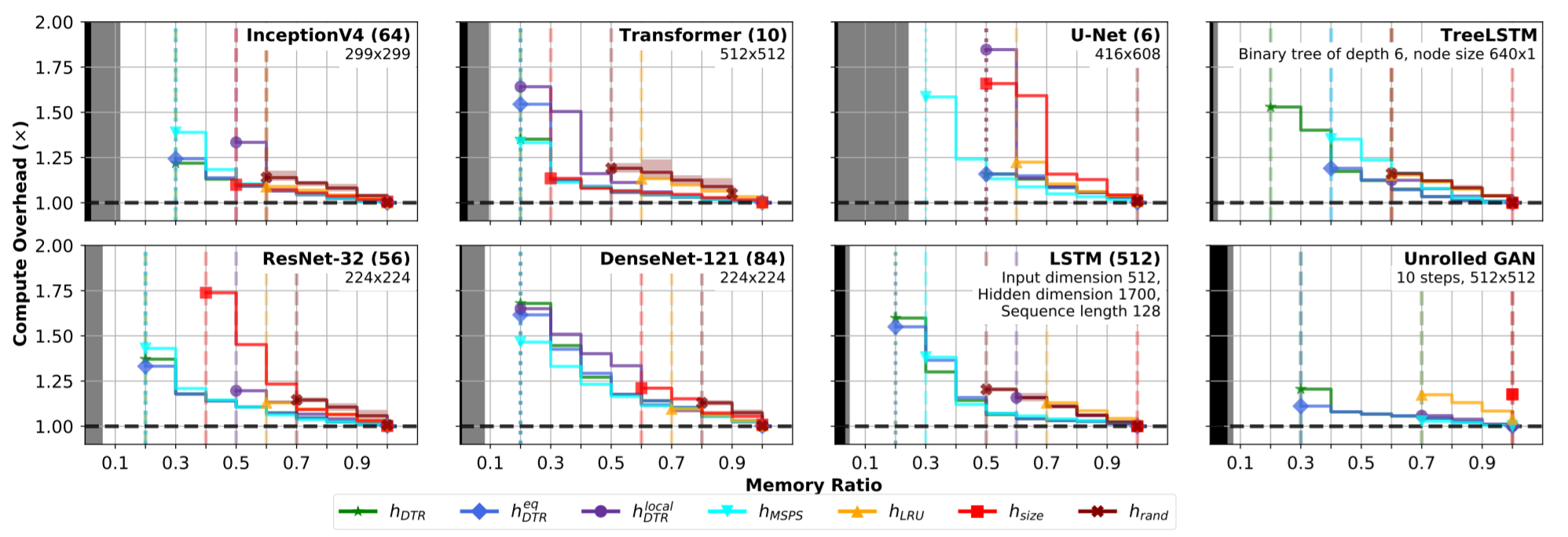
图4:(原文Figure 2)DTR Simulator 在 8 个模型上的测试结果。
图中横坐标是设定的显存阈值,越小代表模型节省的显存越多;纵坐标是计算开销,越低代表计算速度越快。黑色区域代表存储输入和权值变量的显存,灰色部分表示维持当前显存可用需要的空间。共在 7 种 heuristic 下测试了 8 个模型,其中包含 3 种动态模型:LSTM, TreeLSTM, Unrolled GAN。
结果显示,对所有模型,考虑了“上下代” tensor 代价的 heuristics ($h_{DTR}, h_{DTR}^{eq}, h_{MSPS}$) 可允许模型在更低的显存下训练,但同时这些复杂的 heuristics 会使计算时间增加。综合来看,$h_{DTR}^{eq}$ 既保证了最小显存,又权衡了计算时间,因此较为实用。
Fig. 12.
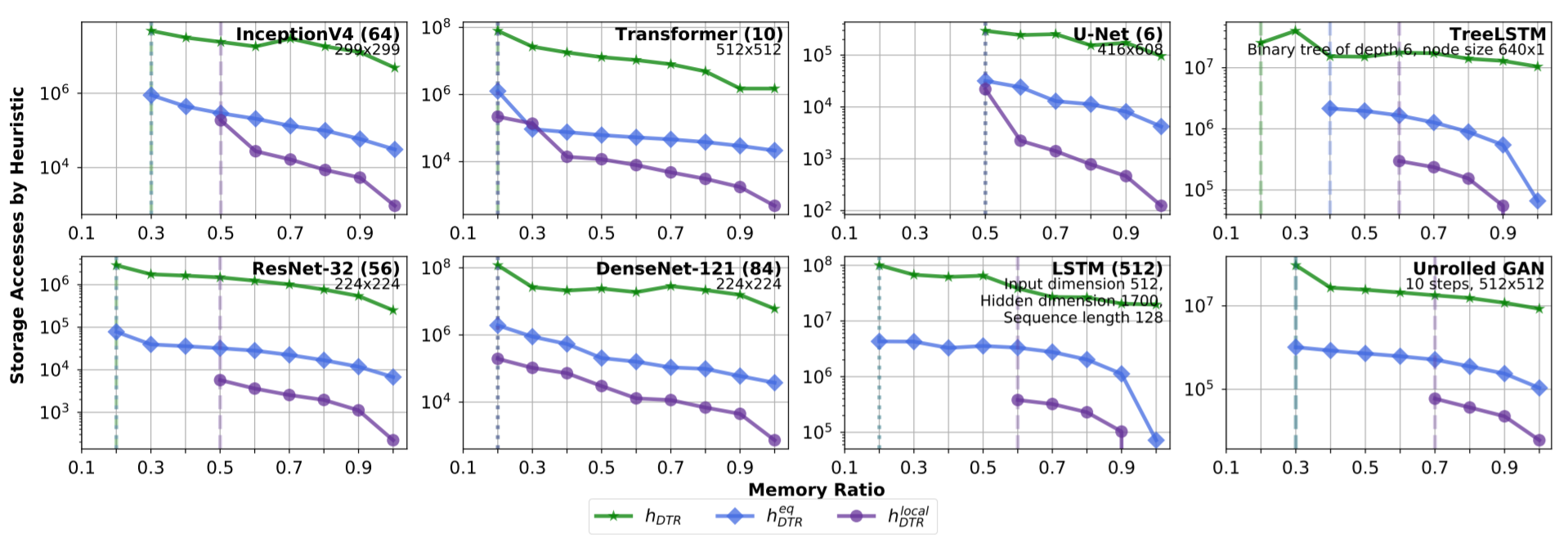
图5:(原文Figure 12)三种 heuristics 下地址访问次数。
原文图 12 展示了 3 种 heuristic 策略在训练 8 个模型时总计需要的地址访问次数,反映了实现这 3 种 heuristic 的复杂度。其中 $h_{DTR}^{local}$ 需要的次数最少,但节省的显存也最少。$h_{DTR}$ 需要访问内存的次数最多。$h_{DTR}^{eq}$ 的地址访问次数居中,节省的显存也与表现最优的 $h_{DTR}$ 相近。
总结
以上是我对 DTR 的全部理解,包含 DTR 的应用背景、基本原理、实现过程和结果。
希望大家能有所收获!
参考
https://zhuanlan.zhihu.com/p/375642263
Ravi Kumar, Manish Purohit, Zoya Svitkina, Erik Vee, and Joshua Wang. Efficient rematerialization for deep networks. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d Alché-Buc, E. Fox, and R. Garnett (eds.), Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019. URL https://proceedings.neurips.cc/paper/2019/file/ ffe10334251de1dc98339d99ae4743ba-Paper.pdf. ↩
Xuan Peng, Xuanhua Shi, Hulin Dai, Hai Jin, Weiliang Ma, Qian Xiong, Fan Yang, and Xuehai Qian. Capuchin: Tensor-based gpu memory management for deep learning. In Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS ’20, pp. 891–905, New York, NY, USA, 2020. Association for Computing Machinery. ISBN 9781450371025. doi: 10.1145/3373376.3378505. URL https://doi.org/10.1145/3373376.3378505. ↩
